Mit dem Brexit und der Trump-Wahl geriet die empirische Umfrageforschung in die Kritik. Schließlich hat keine Prognose im Vorfeld die beiden Ergebnisse sicher vorhergesagt. Kann den Forschern überhaupt getraut werden? Ein detaillierter Blick auf die forschungstheoretischen Grundlagen der empirischen Forschung gibt hier eine klare Antwort.
Aus streng definitorischer Sicht ist Messen in der Statistik bzw. empirischen Sozialforschung definiert als Prozess der Datenerhebung, das heißt der Zuordnung von Zahlen zu Objekten oder Ereignissen nach festgelegten Regeln. In einer weiter gefassten Bedeutung, bei der die Generierung von Aussagen über gemessene oder messbare Zustände, Ereignisse oder Ähnliches ebenfalls als „Messergebnis“begriffen wird, kommen wir nicht umhin, die in letzter Zeit aufgetretenen und in der Öffentlichkeit als „Falschmessungen“ wahrgenommenen Ergebnisse, wie beispielsweise die Prognosen zur letzten US-Wahl oder zur Brexit-Abstimmung in Großbritannien, zur Kenntnis zu nehmen.
Unseres Wissens gibt es keine Definition
des Begriffs „repräsentativ“, vermutlich nicht
einmal ein allgemeingültiges Verständnis.
Wie aber verhält es sich damit bei genauerer Betrachtung? Lassen sich verschiedene Ereignisse, wie hier der Wahlforschung, mit dem Instrumentarium der Umfrage womöglich gar nicht mehr messen? Sind, um bei den Beispielen zu bleiben, Prognosen bei sehr kleinen Unterschieden (im Falle einer dichotomen Entscheidung für oder gegen den Brexit sehr nahe an 50 Prozent liegende Verteilungen) nicht messbar?
Die Beantwortung dieser Frage führt zu der Beobachtung, dass nicht alles, was bei infas als Standard fest verankert ist, im Bewusstsein der Öffentlichkeit und auch bei Nutzern von Statistiken bekannt bzw. in Vergessenheit geraten ist.
Wesentliche Punkte sind dabei die Transparenz aller Schritte, Informationen über den Datenerhebungsprozess und die Reichweite der gemessenen Befunde, was insbesondere auch die korrekte Angabe über die Intervalle der Schätzungen umfasst.
Am Anfang steht dabei die Stichprobe. Voraussetzung für eine saubere Messung ist eine saubere Stichprobe, das heißt in unserem Verständnis eine Wahrscheinlichkeitsauswahl mit bekannten und berechenbaren Auswahlwahrscheinlichkeiten. Idealerweise deckt die Auswahlgrundlage der Stichprobe die Population dabei vollständig ab. Die Stichprobe, ihr Design und Konzept sind also für die Beurteilung und Einordnung der gemessenen Ergebnisse zentral. Der häufig verwendete pauschale Hinweis auf eine „repräsentative Stichprobe“ ist da nicht ausreichend. Zumindest so lange nicht, wie der Begriff keine hinreichende Definition enthält. Unseres Wissens gibt es keine eindeutige Definition des Begriffs „repräsentativ“, vermutlich nicht einmal ein allgemeingültiges Verständnis. Als Hilfe zur Beurteilungder Ergebnisse taugt eine solche pauschale Information nicht.
Neben allen Aspekten der Stichprobenziehung, zu denen selbstverständlich auch deren Umfang gehört, sind folgend auch alle weiteren Schritte im Prozess der Datenerhebung relevant. Dazu zählt als ein Punkt auch das Messinstrument. Auch hier können kleine Variationen große Auswirkungen haben.
Ebenfalls relevant ist die Abarbeitung der gezogenen Stichprobe. Hierbei gewinnt in der Umfrageforschung zunehmend das Problem der Erreichbarkeit an Bedeutung. So lässt sich mit einiger Evidenz feststellen, dass nicht (nur) die Teilnahmebereitschaft deutlich abnimmt, sondern mindestens ebenso deutlich sinkt die Erreichbarkeit. Es wird zunehmend aufwendiger, die zu befragenden Personen überhaupt erst zu erreichen. In diesem Zusammenhang bekommt dann auch die Dauer des Datenerhebungsprozesses eine zentrale Bedeutung. Je länger sie dauert und je kontrollierter sie stattfindet, mit dem Ziel möglichst jeden zu erreichen, desto geringer wird eine Verzerrung aufgrund von sozialgruppenspezifisch selektiven Erreichbarkeiten. Beispielsweise sind Einpersonenhaushalte im Mittel schwerer erreichbar als Mehrpersonenhaushalte. Damit sind aber weitere Merkmale verknüpft, die möglicherweise relevant für das zu messende Ereignis sind. Das ist auch einer der Gründe, warum bundesweite Telefonstichproben bei infas seit einiger Zeit standardmäßig nicht nur aus Festnetz-, sondern auch Mobilfunkstichproben bestehen. So wird nicht nur die Erreichbarkeit von Personen ohne einen Festnetzanschluss überhaupt erst ermöglicht (Coverage-Problem), sondern auch die Erreichbarkeit von hochmobilen Personen und damit auch deren Repräsentanz in der realisierten Stichprobe erhöht.
Am Ende des Datenerhebungsprozesses werden dann die Daten nicht einfach als gemessenes Ergebnis ausgezählt, sondern es erfolgt eine Gewichtung der Daten. Neben der zwingend notwendigen Designgewichtung zum Ausgleich der Auswahlwahrscheinlichkeiten erfolgt üblicherweise eine wie auch immer geartete Anpassung zum Ausgleich von Nonresponse (als Nonresponse-Gewichtung oder als Randanpassung). Auch hier ist das Vorgehen für die Ergebnisse von erheblicher Bedeutung und mehr als nur eine Randnotiz im gesamten Prozess. In der Regel reduziert die Gewichtung zwar den Bias, vergrößert aber den Stichprobenfehler und ist für die Genauigkeit der Schätzung auf Basis der dann gewichteten Ergebnisse von Bedeutung. In der Regel vergrößert eine Gewichtung das Intervall um das geschätzte Ergebnis. infas versucht diesen Tradeoff anzugehen, indem die Gewichtung nicht als einfaches Standardverfahren implementiert ist, sondern je Untersuchung spezifisch bedacht und bearbeitet wird. Hierbei gilt als grundsätzliches Ziel, so viel wie nötig (zur Reduktion des Bias) und so wenig wie möglich (um den Stichprobenfehler nicht unnötig zu vergrößern).
Der kleine Überblick enthält nicht alle, aber einige zentrale Punkte im Prozess der Datenerhebung zur Messung eines Untersuchungsgegenstandes. Um bei den anfangs zitierten Beispielen zu bleiben, ist es sinnvoll, einen zentralen Aspekt näher zu betrachten, nämlich den Stichprobenumfang. Wie groß müsste dieser sein, um aus den gemessenen Ergebnissen zum Brexit auf den Ausgang der Wahl schließen zu können? Einer Abstimmung also, bei der ein Kopf-an-Kopf-Rennen erwartet wurde. Wie groß müsste die Stichprobe, also die Anzahl der Befragten sein, um das Intervall der gemessenen Schätzung auf Basis einer Befragung im Bereich von +/- 1 Prozentpunkten bzw. noch genauer im Bereich von +/- 0,5 Prozentpunkten zu halten?
Diese Frage führt zu den beiden in der Statistik bekannten Fehlentscheidungen, der Fehler 1. Art und der Fehler 2. Art. Sehr vereinfacht auf das vorliegende Problem bezogen, bedeutet der Fehler 1. Art (Nullhypothese = es gibt weniger Brexit-Befürworter als -Ablehner, die zur Wahl gehen), dass eine Entscheidung für den Brexit erkannt wird, obwohl keine Entscheidung für den Brexit stattfinden wird. Der Fehler 2. Art wäre dann, dass eine Entscheidung für den Brexit nicht erkannt wird, obwohl bei der Wahl für den Brexit gestimmt wird. Beide Fehler hängen mit der Fallzahl zusammen. Vereinfacht ausgedrückt, je höher die Fallzahl, desto geringer die Wahrscheinlichkeit, einen Fehler zu begehen. Die statistische Power bezeichnet die Wahrscheinlichkeit, einen Fehler 2. Art zu vermeiden, und lässt sich für die Berechnung einer notwendigen Fallzahl bei hypothesentestenden Fragestellungen verwenden, die groß genug ist, um mit einem bestimmten Fehler auch sehr kleine Unterschiede erkennen zu können. Steht nicht der Nachweis einer Hypothese im Mittelpunkt, sondern die Schätzung eines Populationsparameters, dann kann eine Strategie der Fallzahlplanung zur Abschätzung der erwarteten Breite von Konfidenzintervallen verfolgt werden.
Allerdings scheint diese Berechnung im Vorfeld ein wenig aus der Mode gekommen zu sein. Bisweilen gibt es die Angabe eines Konfidenzintervalls, also eines Bereiches, in dem die Schätzung mit einer bestimmten Wahrscheinlichkeit liegt. Dieses ist abhängig vom Schätzergebnis, im Falle eines Schätzwertes von 50 Prozent ist es am größten. Zudem ist auch das Stichprobendesign für die Intervallbreite relevant.
Wie groß müsste der Stichprobenumfang
sein, um aus den gemessenen Ergebnissen
zum Brexit auf den Ausgang der Wahl
schließen zu können?
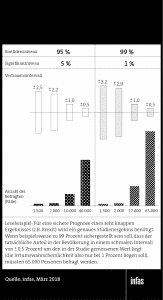
Gehen wir bei einem gemessenen Wert von 50 Prozent für den Brexit und damit der Vorhersage eines exakten Gleichstands von einer einfachen uneingeschränkten Zufallsauswahl (simple random sampling) aus. Unterstellen wir zudem eine intensiv bearbeitete Stichprobe mit einer ausreichenden Feldzeit und vernachlässigen die Effekte einer aufgrund von selektivem Nonresponse möglicherweise notwendigen Gewichtung. Dann ergeben sich bei einem gewählten Konfidenzniveau von 95 Prozent, entsprechend einem Signifikanzniveau von 5 Prozent (vereinfacht, die Wahrscheinlichkeit, eine Entscheidung gegen den Brexit fälschlicherweise zu verwerfen) folgende Vertrauensintervalle:
+/- 1 Prozentpunkte Intervall: rund 10.000 Fälle.
+/- 0,5 Prozentpunkte Intervall: rund 40.000 Fälle.
Bei einem Signifikanzniveau von 1 Prozent, d.h. bei einer deutlich geringeren Wahrscheinlichkeit, einen Fehler zu begehen, ergibt sich eine notwendige Fallzahl von:
+/- 1 Prozentpunkte Intervall: 17.000 Fälle.
+/- 0,5 Prozentpunkte Intervall: rund 65.000 Fälle.
Diese Vertrauens- oder Konfidenzintervalle geben den Bereich an, der bei unendlicher Wiederholung mit einer bestimmten Wahrscheinlichkeit, dem Konfidenzniveau, den wahren Wert einschließt. Das Konfidenzniveau gibt an, wie viel Prozent aller auf Grundlage von gemessenen Daten berechneten Vertrauensintervalle (bei der Berechnung ein und desselben Vertrauensintervalls) den wahren Wert in der Population umfassen.
Am Rande bemerkt sei, dass aufgrund des US-amerikanischen Wahlsystems eine solche Fallzahl in allen 52 Bundesstaaten der USA notwendig wäre, um für jeden Staat die Entscheidung für oder gegen Trump/Clinton bei einer Kopf-an-Kopf-Entscheidung in jedem Bundesstaat mit einer solchen Genauigkeit bzw. in einem derart geringen Intervall zu messen.
Das reale Ergebnis der Abstimmung über den Brexit war dann auch mit 51,9 Prozent für den Brexit und 48,1 Prozent gegen den Brexit in der Tat sehr eng. Die korrekte Vorhersage entsprechend schwierig. Die üblichen Fallzahlen in der Wahlforschung liegen bei n = 1.000, n = 1.500 und bisweilen auch bei n = 2.000 Befragten. Mit diesen Fallzahlen lässt sich aber das Ergebnis einer derart knappen Entscheidung nicht abschätzen, wie ein Blick auf die „naiven“ Vertrauensintervalle zeigt:
Vertrauensintervalle:
n = 1.500, 95 % Konfidenzniveau: +/- 2,5 %
n = 1.500, 99 % Konfidenzniveau: +/- 3,2 %
n = 2.000, 95 % Konfidenzniveau: +/- 2,2 %
n = 2.000, 99 % Konfidenzniveau: +/- 2,9 %
Demnach liegt selbst bei einer je nach Konfidenzniveau und Fallzahl durchaus deutlich über 50 Prozent liegenden Messung gegen den Brexit das reale Ergebnis von nur 48,1 Prozent bei diesen Fallzahlen (selbst bei einer erlaubten Fehlertoleranz von 5 Prozent) noch innerhalb des Vertrauensintervalls.
Angegeben ist in den obigen Beispielen zudem stets das „naive“ Vertrauensintervall, also das Konfidenzintervall
unter den genannten Bedingungen. In der Umfrage bzw. Wahlforschung kann allerdings eher selten auf eine uneingeschränkte Zufallsauswahl
zurückgegriffen werden und zudem erfolgt in der Wahlforschung (und den meisten Umfrageforschungen) die Gewichtung der Daten standardmäßig. Beides vergrößert den Stichprobenfehler und erhöht damit das Vertrauensintervall unter Umständen erheblich. Auch dies kann und sollte berücksichtigt werden. Die Angabe eines Vertrauensintervalls ohne Berücksichtigung des tatsächlichen Stichprobendesigns inkl. Gewichtung ist andernfalls ebenfalls irreführend.
Betrachten wir die Fallzahlen, wird klar, dass viele der in der Öffentlichkeit als „Falschmessungen“ wahrgenommenen Ergebnisse streng genommen nicht wirklich falsch waren. Sie waren lediglich zu ungenau, was aber nicht immer erkennbar wurde. Knappe dichotome Entscheidungen sind also durchaus schwierig zu messen und stellen die Forschung (hier die Wahlforschung) vor Probleme, die nur mit einigem Aufwand bearbeitet werden können. Dennoch können sie bearbeitet werden. Um die anfangs gestellte Frage zu beantworten: Aus unserer Sicht lassen sich mit dem Instrumentarium der Umfrageforschung auch Ereignisse mit sehr kleinen vermuteten Unterschieden messen. Allerdings ist das mit erheblichem Aufwand, mit erheblichen Kosten und auch mit Unsicherheiten verbunden.
Zusammengefasst lässt sich sagen, dass es lohnenswert ist, den gesamten Prozess der Datenerhebung sorgfältig zu planen. Im Sinne der Gültigkeit und Zuverlässigkeit der Ergebnisse lohnt es sich, darüber nachzudenken und die Probleme zu benennen. Sicher können nicht immer alle Probleme gelöst werden, aber deren Auswirkungen auf das gemessene Ergebnis lassen sich häufig benennen und sollten dann auch benannt werden. Am Ende bleibt nicht nur die Frage, was habe ich gemessen, sondern auch die Frage, bei wem habe ich gemessen und wie genau habe ich gemessen bzw. erhoben. Eine transparente Darstellung ist dabei sicher ein Schritt, das Vertrauen in die gemessenen Ergebnisse der empirischen Sozialforschung zu stärken.
Zum Weiterlesen:
1 Schnell, Rainer, Noack, M., 2014, The Accuracy of Pre-Election Polling of German General Elections. In: MDA – Methods, Data, Analysis 8 (1) 5-24, http://www.gesis.org/fileadminupload/forschung/publikationen/zeitschriften/mda/Vol.8_Heft_1/MDA_Vol8_2014-1_Schnell_Noack.pdf
2 Schnell, Rainer, Hill, P. B., Esser, E., 2013, Methoden der empirischen Sozialforschung (10. überarb. Aufl.), München, Wien: R. Oldenbourg Verlag.
3Weichbold, Martin, Bacher, J., Wolf, C. (Hrsg.), 2009, Umfrageforschung, Herausforderung und Grenzen, Österreichische Zeitschrift für Soziologie, Sonderheft 9, VS Verlag für Sozialwissenschaften
4Cochran, William G., 1977, Sampling Techniques (3rd Edition), New York: John Wiley & Sons. Leslie Kish, 1965, Survey Sampling, New York: John Wiley & Sons.
Foto: Alyssa Kibiloski

